채린's datascience

Let’s start with an example: Suppose you're given a dataset that contains the size (in terms of area) of different houses and their market price. Your goal is to come up with an algorithm that will take the size of the house as its input and return its market price as the output.

In this example, the input variable i.e the size of the house, is called the independent variable (X), the output variable i.e house price is called the dependent variable (Y), and this algorithm is an example of supervised learning. 

In supervised learning, algorithms are trained using "labeled" data (in this example, the dependent variable - house price, is considered a label for each house), and trained on that basis, the algorithm can predict an output for instances where this label (house price) is not known. "Labeled data" in this context simply means that the data is already tagged with the correct output. So in the above example, we already know the correct market price for each house, and that data is used to teach the algorithm so that it can correctly predict the house price for any future house for which the price may not be known.

The reason this paradigm of machine learning is known as supervised learning, is because it is similar to the process of supervision that a teacher would conduct on the test results of a student on an examination, for example. The answers the student gives (predictions) are evaluated against the correct answers (the labels) that the teacher knows for those questions, and the difference (error) is what the student would need to minimize to score perfectly on the exam. This is exactly how machine learning algorithms of this category learn, and that is why the class of techniques is known as supervised learning.

There are mainly 2 types of supervised learning algorithms:

1. Regression, where your output variable is a continuous variable, for example, the price of a house.
2. Classification, where your output variable is categorical, for example, approve the loan or not i.e. yes or no categories.

In this lecture, we will be learning about regression algorithms, which obviously find great use in the machine learning prediction of several numerical variables we would be interested in estimating, such as price, income, age, etc.

Linear Regression

Linear Regression is useful for finding the linear relationship between the independent and dependent variables of a dataset. In the previous example, the independent variable was the size of the house and the dependent variable its market price.

This relationship is given by the linear equation: 

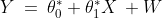
Where 

 is the constant term in the equation, 

 is the coefficient of the variable 

, 

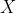
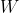
is the difference between the actual value 

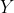
 and the predicted value (

).

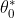
 and 

 are called the parameters of the linear equation, while 

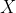
 and 

 are the independent and dependent variables respectively.

What is an error?

With given 

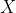
 and 

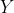
 in the training data, the aim is to estimate 

 and 

 in such a way that the given equation fits the training data the best. The difference between the actual value and the predicted value is called the error or residual. Mathematically, it can be given as follows:

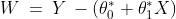
In order to estimate the best fit line, we need to estimate the values of 

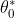
 and 

  which requires minimizing the mean squared error. To calculate the mean squared error, we add the square of each error term and divide the sum with the total number of records: 

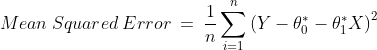
The equation of that best fit line can be given as follows: 

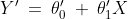
Where 

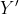
 is the predicted value, 

 are the estimated parameters.

This equation is called the linear regression model. The above explanation is demonstrated in the below picture:

Before applying the model over unseen data, it is important to check its performance to make it reliable. There are a few metrics to measure the performance of a regression model.

1. R-squared: R-squared is a useful performance metric to understand how well the regression model has fitted over the training data. For example, an R-squared of 80% reveals that 80% of the training data fit the regression model. A higher R-squared value generally indicates a better fit for the model.
   
   
2. Adjusted R-squared: The adjusted R-squared is a modified version of R-squared that takes into account the number of independent variables present in the model. When a new variable is added, adjusted R-squared increases if that variable adds value to the model, and decreases if it does not. Hence, adjusted R-squared is a better choice of metric than R-squared to evaluate the quality of a regression model with multiple independent variables, because adjusted R-squared only remains high when all those independent variables are required to predict the value of the dependent variable well; it decreases if there are any independent variables which don't have a significant effect on the predicted variable.
   
   
3. RMSE: RMSE stands for Root Mean Squared Error. It is calculated as the square root of the mean of the squared differences between actual outputs and predictions. The lower the RMSE the better the performance of the model. 
   Mathematically it can be given as follows: