Cox proportional hazard regression은 여러 변인들에 의해 생준율의 영향을 설명할 수 있고 여러 변수를 추가하여 설명할 수 있는 모형이다. 여러 Survival 분석 중 하나의 비모수적 방법이다. 주로 의학에서 자주 사용되고 임상실험에 대한 분석을 할 때 믿음직스럽게 사용된다. 생존분석은 사건이 발생까지의 시간과 사건의수로 사건발생률을 계산한다.
Hazard function
일단, Hazard function(위험함수)에 대해서 짚고 넘어간다.
hazard는 위험률을 말하는데 어느 시점에 대상이 탈락가능성이 높은지 평가하는 비율이다.
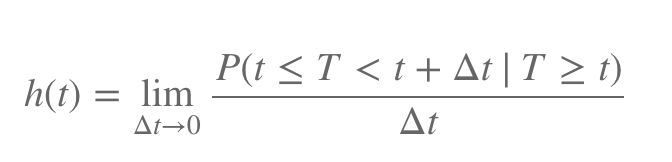
위 함수에서 확률부분은 t시점까지 살아남은 대상이 다음 델타t시간안에 죽을 조건부확률이다. 이를
델타t로 나누면 단위시간당 죽을 확률이된다. 이에 극한개념을 대입하면, 특정 t에서
순간 위험률함수를 나타낼 수 있다. 이것이 hazard function, h(t)이다.
생존함수는 대상이 얼마나 오래 살아있는가를 나타내는 반면,
위험률함수는 특정 시점에 죽을 가능성을 나타낸다.
따라서, 어떤 event가 발생할 위험률 함수로 쓰이며, 생존분석에서 통계모형을 나타내는 다양한 용도로 쓰인다.
그것들 중 Cox PH model에 대해서 알아본다.
Cox PH model
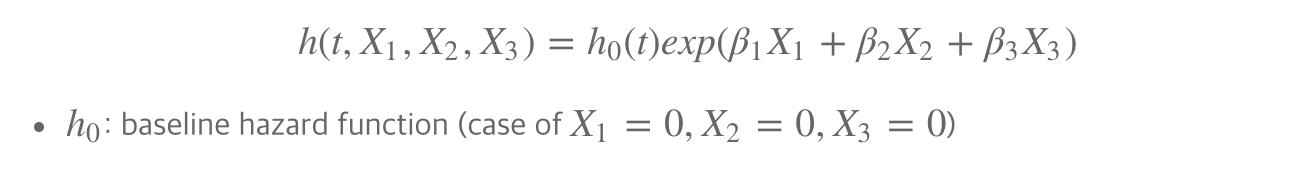
여기서 각 변수앞에 붙은 계수들은 당연히 변수와 관계가 있다.
이때 위험률 비를 구하면, 두군에 대해서 각각 위험률 함수를구하고 이를 나누면 hazard ratio라고 한다.
Hazard ratio
예를들어 담배가 X변수이고 암이 event라고 했을 때,
담배를 피지 않는 집단 X =0 과 담배를 피는 집단 X=1 의 hazard ratio를 각각 구해 둘을 나눈 비를
hazard ratio라고 한다.
예를 들어 이 값이 2.8이라고 하면,
직관적인 해석으로는 '담배를 피는 사람은 피지 않는 사람에 비해 2.8배 위험성이 높다는 것'이다.
각각 X1에 의한 hazard function은 아래와 같고
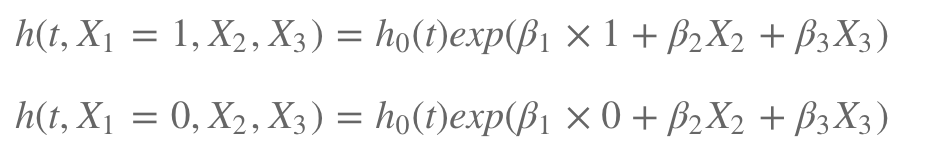
이로부터 hazard ratio를 구하면 다음과 같이 된다.

이때, h0(t)는 나누면서 사라지기 때문에 베타를 해석하는데 아무런 영향을 주지 않는다.
또한 시간은 h0(t)에만 영향을 미치기 때문에, 시간이 흘러도 hazard ratio는 변하지 않는다.
시간에 따라 hazard function의 값이바뀔 수는 있어도 비율은 달라지지 않는다.
이런 가정을 만족시키는 데이터에 대해서 이 모형을 사용할 수 있다.
Adjusted Survival Curves
우리는 이와같은 학습을 통해 유저의 생존곡선을 그리려고 한다.
여러 변수들의 특성을 적용하여 모형으로 쉽게 나타낼 수 있다.
참고문헌:
https://boxnwhis.kr/2015/04/24/drawing_survival_curves_with_predictors.html
설명 변수를 이용하여 유저 생존 곡선 그리기
설명 변수를 이용하여 유저 생존 곡선을 그립니다. Cox PH model을 활용합니다.
boxnwhis.kr
생존분석에 대해 정리가 잘 된 페이지를 소개한다.
https://statkclee.github.io/ml/ml-pm-survival.html
xwMOOC 기계학습
statkclee.github.io
http://statkclee.github.io/parallel-r/
Software Carpentry: R 병렬 프로그래밍
“AI is a superpower!!!”, 인공지능을 체득하면 슈퍼파워를 손에 쥘 것이다. Andrew Ng 금수저, 은수저 슈퍼파워를 받은 사람과 기계학습을 통달한 흑수저들간의 무한경쟁이 드뎌 시작되었다. 물론, 금
statkclee.github.io
'통계분석 > 의학통계' 카테고리의 다른 글
| 생존분석 - harrell's C-index (2) | 2022.10.24 |
|---|---|
| 두군의 수가 맞지 않을때: Propensity Score Matching and univariate Cox ph regression (0) | 2021.05.10 |
| Cox proportional hazard regression HRplot해석 (0) | 2020.10.21 |