Continuous and Categorical variables
A continuous variable can take an infinite number of distinct numerical values, possibly in a given range of numbers. For example, the Monthly Income of employees in a certain firm is a continuous variable.
A categorical variable, on the other hand, can take only a limited (finite) number of distinct values. For example, in an image dataset of single handwritten digits, the digit in the image would be a categorical variable because it can only take a finite number of distinct values, in this case from 0 to 9, and nothing beyond that.
Dependent and Independent Variables
In data science, given a set of variables, we need to establish the relationship between one variable and others. The variable to be estimated is dependent on the rest of the variables and hence called the dependent variable, while the remaining variables that affect the dependent variable are called independent variables.
For example, if we have 4 features Age, Education Level, Work Experience, and Salary, and need to find the relation between the Salary and the rest of the features, the Salary would be the dependent variable while Age, Education Level, and the Work Experience would be independent variables.
Variance and Standard Deviation
In statistics, it is important to understand the magnitude of the spread of the observed data from the Mean.
Variance and Standard Deviation are two quantities that address this concept. To calculate the variance, we take the difference between each number in the dataset and the mean of the data, square this difference to make it positive (independent of sign), and finally divide the sum of the squares by the total number of values in the dataset.
Mathematically, the variance of the population can be given as follows:
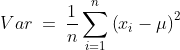
Where
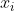
is a data point,
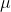
is the population mean, and
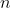
is the total number of data points.
One of the major drawbacks of using variance, to understand the spread of the data, is its interpretability. The unit of variance is the square of the original unit of the data. To overcome this, another quantity is introduced, which is the square root of the variance. This is called the standard deviation of the population.
Mathematically, the standard deviation of the population can be given as follows:
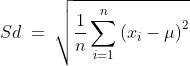
Being the square root of the variance, the standard deviation is more interpretable, having the same units as the original data points. The standard deviation is able to give a sense for the measure of the spread of the dataset around its mean.
Confidence Interval
Inferential statistics is associated with estimating the population parameters by extracting samples from the same population. In general, when we make an estimate about some quantity of the population (for example, mean), we come up with a single number. This single number is called a point estimate. For example, if we take a sample from a population and the sample mean is 35, then it is expected that the population mean is also 35. The drawback of point estimates is that we do not know how sure we are that the population mean is 35.
To increase the certainty of our estimate, we associate it with another concept known as the confidence interval.
A confidence interval is a range of values from the point estimate, where we assume that the population parameter will lie in this range with a certain percentage of confidence.
Let’s consider an example: Suppose we are extracting 100 samples from a group of students in a university, where each sample has a certain number of records. We have calculated the mean age of students from each sample. Now, if we say that the confidence interval is [18, 24] with a 95% probability, then it means that the mean age of 95 out of 100 samples will lie in the range of 18-24.
The higher the confidence, the more the width of the confidence interval.